Pump Efficiency Explained

In this post, we'll break down the meaning of pumping efficiency so we have a clear understanding of what's being measured, what the numbers mean, and how it can affect your farming operations.

Efficiency

Suppose we have a bushel of apples to move across a field.

The work output we want is getting the apples from where they are across the field and into the shed.

To do this, we could drag the bushel across the ground.  We'd eventually get the apples to the shed, but it would be hard and tiring.

Another way to do this would be to put the apple bushel in a wagon.

The work output hasn't changed.  We are still moving the same amount of apples from the same starting point to the same ending point.  But this time it's easier because the work we have to put in to get the wagon to move is much lower than the work we have to put in to drag the bushel.  That is to say, the wagon is more efficient than dragging the bushel.

As an engineering concept, mechanical efficiency is generally defined as the ratio of work output by a system to the work put into the system.  It is a percentage, and it can never be greater than 100%.

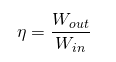
Since work and energy are equivalent, it is just as correct to say that mechanical efficiency is equal to the ratio of work output by a system to energy put into it:

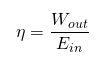
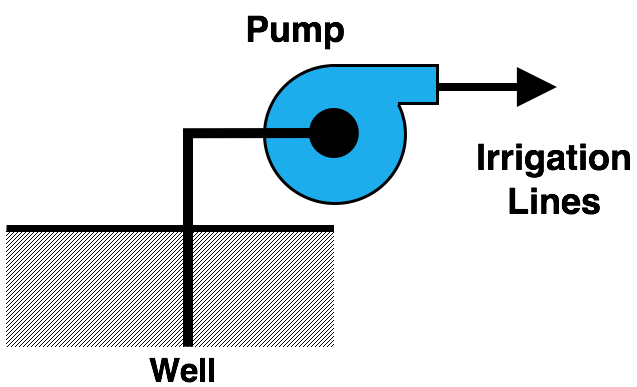
Irrigation Pumps

Energy input

Irrigation pumps require an energy source to move water.  This is typically an electric motor these days, although some pumps still have internal combustion engines as a power source.  In the case of electric motors, we tend to measure the energy put into them in kilowatt-hours (kWh).

Work output

Conceptually, the job of an irrigation pump consists of getting the water from where it is to where you need it to be.  The work it does is defined by the quantity of water being moved, and the difficulty involved in moving that water.  The quantity of water in an agricultural setting is usually thought of in acre-feet, a unit of volume (V).  The difficulty to move the water is referred to as total dynamic head (h).  We also need a constant (k) to make the units of measure agree, since efficiency is a percentage. Then the equation becomes

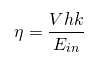
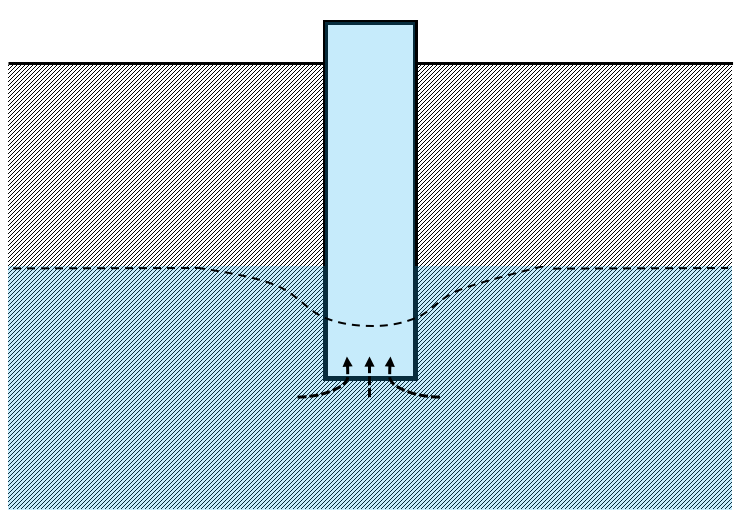
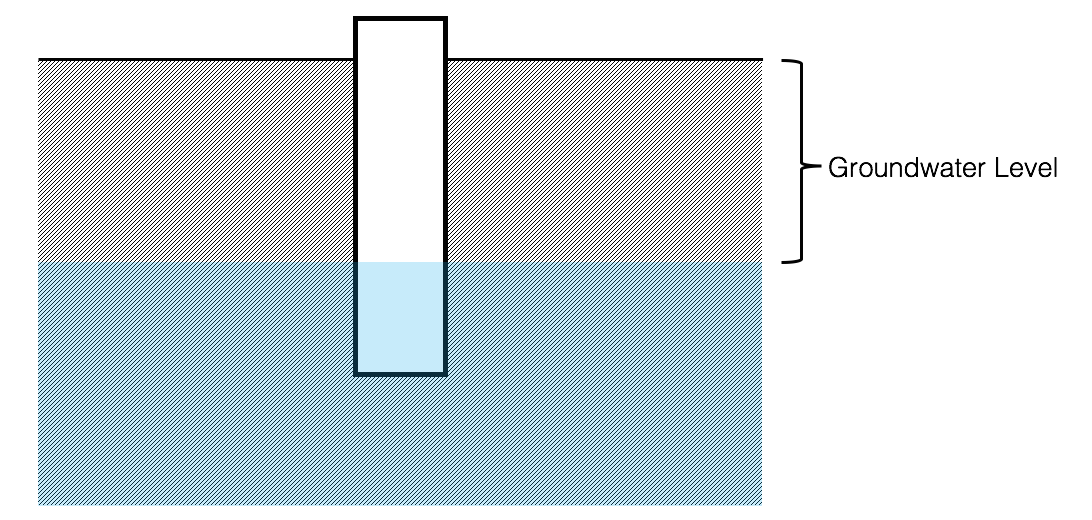
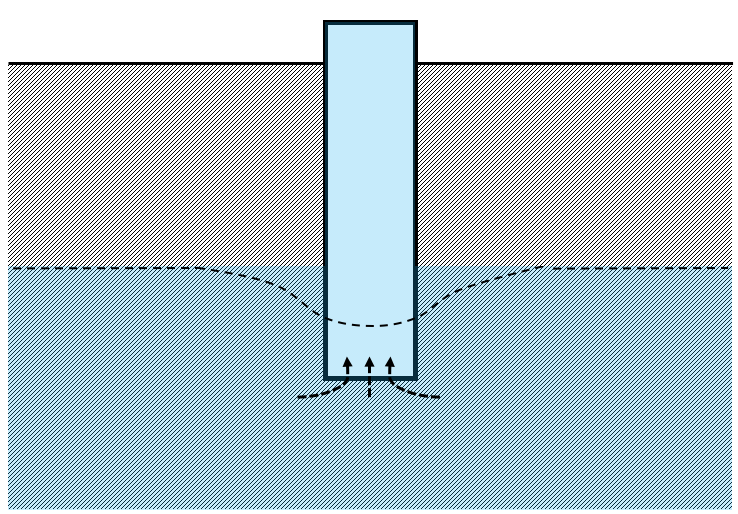
Total dynamic head

Total dynamic head for a groundwater pump can be broken apart into a few pieces of information that are provided on pump test reports:

• • Standing water depth (h_s) - this is the depth to water from the ground surface when water isn't being pumped.  You can get this number by dropping a tape down your well when it's not being pumped.  This will change as conditions in the aquifer change.

• • Drawdown (h_dd) - this is the amount that the water level locally drops when the pump is actually running.  This is dependent on the soil conditions around the water level; in a cavern aquifer drawdown would be essentially zero, while in sand or sandstone it might be dozens of feet or more.

• • Discharge head (h_di) - this is the extra difficulty the water has to overcome after leaving the pump before it exits the drip heads or spray nozzles.

• Sometimes instead of this number, the supply pressure (P) will be listed, in which case (for pressures in psi)
  • 

Then the total dynamic head is given by

The constant

With energy input in units of kWh, head in feet of water, and volume in acre-feet,

Putting it all together

This brings us to our final form of the pumping efficiency equation for irrigation pumps:

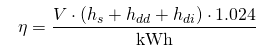
Thanks for hanging with us throughout this educational series. We hope you learned something and can apply it on your farm to drive energy and water savings!

Nathan Taylor, P.E. is a mechanical engineer and an Energy Analyst with Wexus Technologies, Inc. Nate eats energy and water data for breakfast and is an expert at dodging car and foot traffic while riding his scooter in San Francisco.